Boolean Logic, Truth Tables and Karnaugh Maps

• Boolean Algebra #1
• Boolean algebra #2: Basic problems
• Boolean algebra #3: Basic problems
• Boolean algebra #4: Different terminology and notations
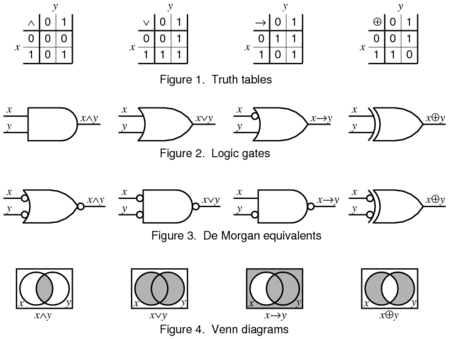
• Boolean algebra #5: Truth tables - introduction
• Boolean algebra #6: Truth tables - variables combinations
• Boolean algebra #7: Truth tables - example problems
• Boolean algebra #8: Truth tables - into expressions/statements
• Boolean algebra #9: truth tables - into expressions (continued)
• Boolean algebra #10: Truth tables - example

• Boolean algebra #11: Truth tables - example (continued)
• Boolean algebra #12: Karnaugh maps
• Boolean algebra #13: Karnaugh maps example (continued)
• Boolean algebra #14: Karnaugh maps - short summary
• Boolean algebra #15: Karnaugh maps - from expressions
• Boolean algebra #16: Karnaugh maps - from expressions (continued)
• Boolean algebra #17: Karnaugh maps - grouping
• Boolean algebra #18: Karnaugh maps - grouping (continued)
• Boolean algebra #19: Karnaugh maps - getting the result
• Boolean algebra #20: Karnaugh maps - getting the result (continued)
• Boolean algebra #21: Karnaugh maps - getting the result (continued)
• Boolean algebra #22: Karnaugh maps - final example
• Boolean algebra #23: DeMorgan's theorem - introduction
• Boolean algebra #24: DeMorgan's theorem - examples
• 
  Boolean algebra #25: DeMorgan's theorem - examples (continued)
• Boolean algebra #26: Sum of products (SOP) form
• Boolean algebra #27: Standard SOP form
• Boolean algebra #28: Standard SOP form (continued)
• Boolean algebra #29: Product of sums (POS) form
• Boolean algebra #30: Product of sums (POS) form (continued)
Web Tutorials
• Karnaugh Maps 1
• Karnaugh Maps 2
  

• Karnaugh Maps 3
  

Simplification of Boolean Logic

Boundedness Law

X + 1 = 1

X . 0 = 0

Absorption Law

X + (X . Y) = X

X . (X + Y ) = X

Elimination Law

 X + (X' . Y) = X + Y

X.(X' + Y) = X.Y

Unique Complement theorem

If X + Y = 1 and X.Y = 0 then X = Y'

Involution theorem

 X'' = X

0' = 1

Associative Properties

X + (Y + Z) = (X + Y) + Z

X . ( Y . Z ) = ( X . Y ) . Z

Duality Principle

Interchanging AND and OR operators and replace 0's by 1's and 1's by 0's.

Duality of X.Y+Z' = (X'+Y').Z

Minterms and Maxterms
Any boolean expression may be expressed in terms of either minterms or maxterms.

Literal
A literal is a single variable within a term which may or may not be complemented.

A minterm is the product of N distinct literals where each literal occurs exactly once.

A maxterm is the sum of N distinct literals where each literal occurs exactly once.

The minterms and maxterms for a two-variable expression is
A  B   Minterm  Maxterm
0   0   A'.B'       A+B
0   1   A'.B        A+B'
1   0   A.B'        A'+B
1   1   A.B         A'+B'

The minterms and maxterms for a three variable expression is
A B C Minterm  Maxterm
0  0 0 A'.B'.C'    A+B+C
0  0 1 A'.B'.C     A+B+C'
0  1 0 A'.B.C'     A+B'+C
0  1 1  A'.B.C    A+B'+C'
1   0 0 A.B'.C'   A'+B+C
1   0 1 A.B'.C   A'+B+C'
1   1  0 A.B.C'  A'+B'+C
1   1 1  A.B.C   A'+B'+C'